今期と元期の座標を考える必要が出てきたのは、電子基準点の成果座標(元期座標)そのままでは、新点を求める平均計算の計算精度の確保が難しくなってきたためです。

イメージで説明してみます。

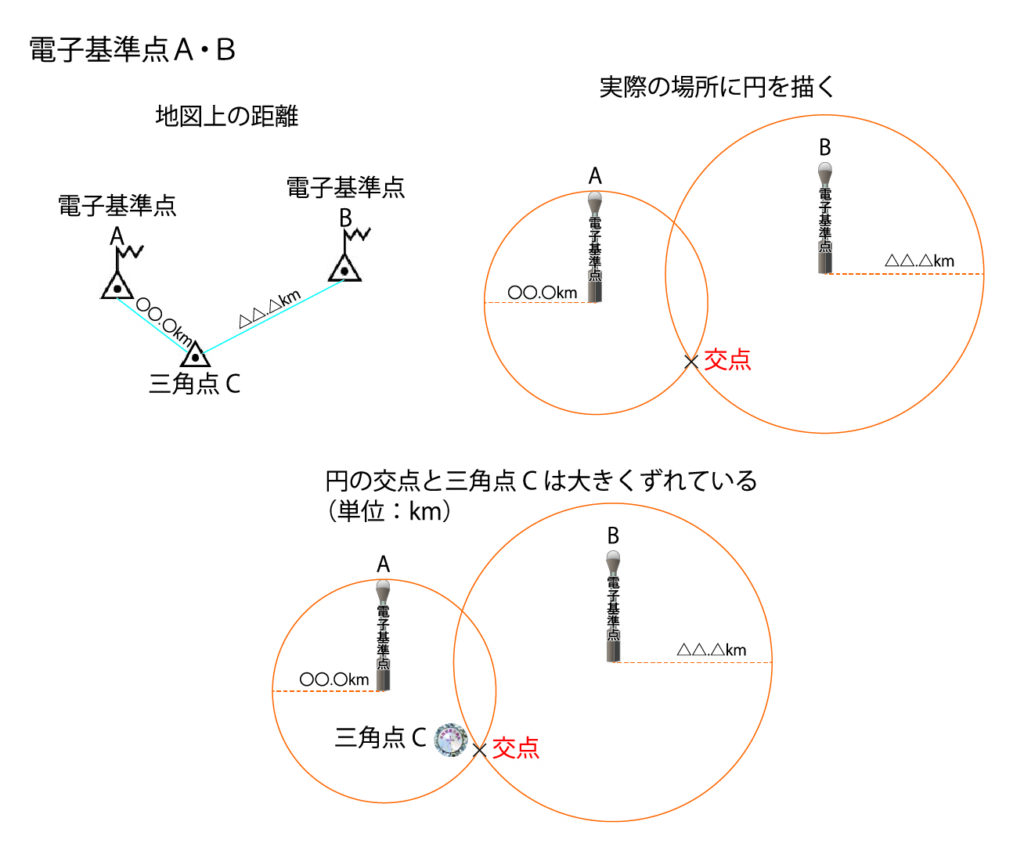
地図上の三角点Cが、電子基準点Ａからの距離が地図上で〇〇.〇km、別の電子基準点Ｂからの距離が地図上で△△.△kmであったとします。
この条件下で、(地図上ではなく実際の)電子基準点Ａから〇〇.〇kmを半径とする円 と 電子基準点Ｂから△△.△kmを半径する円を描けたとすると、三角点Cはこの２つの円の交点になるはずです。ですが、そうなりません。

原因は
・日本の国土は、地殻変動になどにより、少しずつでも変化している。
・地図の座標は、ある時期(過去)に測量・測位したもの。頻繁には更新しない。
・地図の座標は、電子基準点の座標に整合する(位置関係に矛盾がない)ように求められている。
などがあります。

三角点Cと交点のずれが大きくなると、新点の計算精度に影響が出て来ることになります。

 

次に、電子基準点Ａ・Ｂではなく、４級基準点Ａ・Ｂで考えてみます。

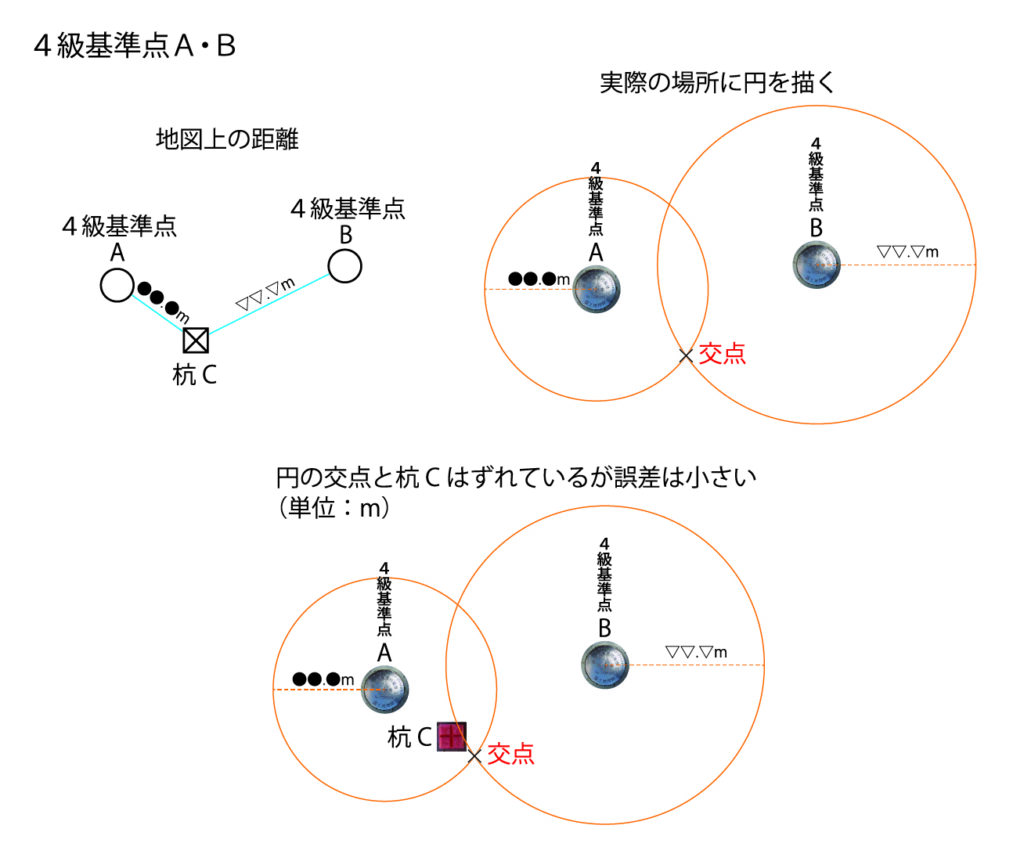
地図上の杭Cは、４級基準点Ａからの距離が地図上で●●.●m、別の４級基準点Ｂからの距離が地図上で▽▽.▽mであったとします。
この条件下で、(地図上ではなく実際の)地上の４級基準点Ａから●●.●mを半径とする円 と 地上の４級基準点Ｂから▽▽.▽mを半径する円を描けたとすると、杭Cはこの２つの円の交点とほぼ同じになるはずです。

違いは、電子基準点間の距離と４級基準点間の距離の差です。
点間距離が離れた2点は、地殻変動の影響を大きく受けます。これが新点の計算精度を落とす要因で、今期座標・元期座標を導入するきっかけです。

・正しく学びたい方は『国土地理院 セミ・ダイナミック補正 導入背景』で検索。

そのため、
既知点を電子基準点のみ(つまり点間距離が離れた)で計算する測量を行う場合には、以下の計算を行い計算精度を高めることになります。

①電子基準点の成果座標(元期座標)から、電子基準点の今期座標を求める。
②電子基準点(今期座標)と新点のベクトルを、基線解析計算で求める。
③新点の座標を三次元網平均計算で求める(今期座標で求まる)。
④求めた新点の今期座標から、元期座標を求める。これが地図上の座標(成果座標)となります。

前提としているのは、
今期座標は『ある時期に求めた元期座標ではなく、今、GNSS測量を行い計算した場合の座標に近い座標』ということです。
そのため、③の計算誤差が小さくなり、結果、④の座標の信頼が高まります。

この計算過程を、セミ・ダイナミック補正計算と呼びます。